Suppose that we store some information on disk and want to check if a certain
file contains a certain entry. Reading from disk is time consuming, so we want
to minimize it as much as possible. A Bloom filter is a data structure that
implements a cache with probabilistic properties:

1. If the cache says the key is not present in a specific file, then it’s
   100% certain we should not be reading the file.
2. If the cache says the key is present in the file, there’s a small chance
   this is a false positive (and in fact the key isn’t there). In this case
   we just read the file as usual.

In a scenario where the majority of queries “is this key in that file?” have a
negative answer, a Bloom filter can significantly speed up the system [1].
Moreover, the probabilistic nature (the existence of false positives) allows
Bloom filters to be extremely fast and occupy very little space. Here’s a quote
from the Bloom paper:

The new hash-coding methods to be introduced are
suggested for applications in which the great majority of
messages to be tested will not belong to the given set. For
these applications, it is appropriate to consider as a unit of
time (called reject time) the average time required to
classify a test message as a nonmember of the given set.

How a Bloom filter works

A Bloom filter is a special kind of a hash table with open addressing.
It’s an array of bits (the length is typically denoted m), and some fixed
number (k) of hash functions. We’ll assume each hash function can take an
arbitrary sequence of bytes and hash it into an integer in the inclusive range
[0, m-1]. A Bloom filter supports two operations:

Insert an item: the item is hashed using each of the k hash functions, and the
appropriate bits in the underlying array are set to 1.

Test if an item is a member: the item is hashed using each of the k hash
functions. If any of the bits indicated by their results is 0, we return “false”
with certainty. If all the bits are 1, we return “true” – and there’s a small
chance of false positives.

Here’s how the Bloom paper describes it:

The hash area is considered as N individual addressable bits, with addresses 0
through N – 1. It is assumed that all bits in the hash area are first set to 0.

Next, each message in the set to be stored is hash coded into a number of
distinct bit addresses, say a1, a2, . . . , ad. Finally, all d bits addressed by
a1 through ad are set to 1.

To test a new message a sequence of d bit addresses,
say a’1, a’2, … a’d, is generated in the same manner as for storing a message.
If all d bits are 1, the new message is accepted. If any of these bits is zero,
the message is rejected.

Hopefully it’s clear why this data structure is probabilistic in nature: it’s
possible that different items hash to the same number, and therefore when
we test some X, all its hashes point to bits turned on by the hashing of other
data. Read the Math appendix for the math behind Bloom filters and how to
calculate (and design for a specific) the false positive rate.

Here’s an example:

1. We start with an empty bloom filter with m=16 and k=3. All bits
   are initialized to 0.
2. Insertion of “x”. The three hashes return indices 1, 6, 15, so these bits
   in the array are set to 1.
3. Insertion of “y”. Hashing returns indices 6, 9 and 13, so these
   bits in the array are set to 1. Note that bit 6 is set for both “x” and “y”,
   and that’s fine.

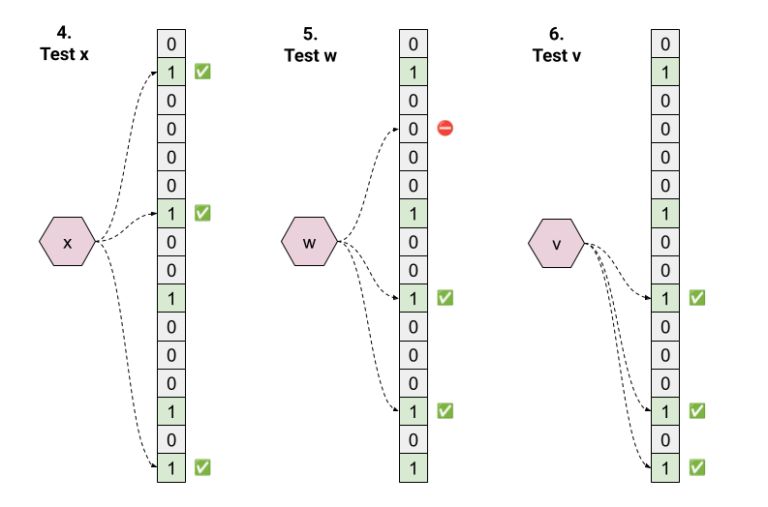
Next, let’s look at some membership tests:

4. Test “x”. Hashing returns 1, 6, 15; all these bits are 1 in the
   array, so the answer is “true”. This is a true positive.
5. Test “w”. Hashing returns 3, 9, 13. Since the bit at position 3 is 0, the
   answer is “false”.
6. Test “v”. Hashing returns 9, 13, 15; all these bits are 1 in the array,
   so the answer is “true”. This is a false positive.

Note that it’s trivial to prove (by the law of contraposition) that all “false”
answers from a Bloom filter’s test operation are true negatives.

Implementation

Here’s a simple implementation of a Bloom filter in Go:

// New creates a new BloomFilter with capacity m, using k hash functions.
// You can calculate m and k from the number of elements you expect the
// filter to hold and the desired error rate using CalculateParams.
func New(m uint64, k uint64) *BloomFilter {
  return &BloomFilter{
    m:      m,
    k:      k,
    bitset: newBitset(m),
    seed1:  maphash.MakeSeed(),
    seed2:  maphash.MakeSeed(),
  }
}

type BloomFilter struct {
  m      uint64
  k      uint64
  bitset []uint64

  // seeds for the double hashing scheme.
  seed1, seed2 maphash.Seed
}

// Insert a data item into the bloom filter.
func (bf *BloomFilter) Insert(data []byte) {
  h1 := maphash.Bytes(bf.seed1, data)
  h2 := maphash.Bytes(bf.seed2, data)
  for i := range bf.k {
    loc := (h1 + i*h2) % bf.m
    bitsetSet(bf.bitset, loc)
  }
}

// Test if the given data item is in the bloom filter. If Test returns false,
// it's guaranteed that data was never added to the filter. If it returns true,
// there's an eps probability of this being a false positive. eps depends on
// the parameters the filter was created with (see CalculateParams).
func (bf *BloomFilter) Test(data []byte) bool {
  h1 := maphash.Bytes(bf.seed1, data)
  h2 := maphash.Bytes(bf.seed2, data)
  for i := range bf.k {
    loc := (h1 + i*h2) % bf.m
    if !bitsetTest(bf.bitset, loc) {
      return false
    }
  }
  return true
}

The bitsetSet and bitsetTest functions can be seen in the
full code repository.

This implementation uses double hashing to
generate k different hash functions from just two hashes.

The code also mentions the CalculateParams function:

// CalculateParams calculates optimal parameters for a Bloom filter that's
// intended to contain n elements with error (false positive) rate eps.
func CalculateParams(n uint64, eps float64) (m uint64, k uint64) {
  // The formulae we derived are:
  // (m/n) = -ln(eps)/(ln(2)*ln(2))
  // k = (m/n)ln(2)

  ln2 := math.Log(2)
  mdivn := -math.Log(eps) / (ln2 * ln2)
  m = uint64(math.Ceil(float64(n) * mdivn))
  k = uint64(math.Ceil(mdivn * ln2))
  return
}

You’ll have to read the Math appendix to understand how it works.

Practicalities

Let’s look at a practical example of a realistic Bloom filter and how it
performs. Suppose we want to store about 1 billion items, and have a false
positive rate of 1% (meaning that if the filter returns “true” for a test,
there’s a 99% chance that the item was previously added to the filter).
Using these requirements, we can invoke CalculateParams to get the Bloom
filter parameters:

CalculateParams(1000000000, 0.01) ===> (9585058378 7)

This means m is about 9.6 billion (bits) and k is 7. In other words, our
Bloom filter requires about 1.2 GB of space to cache the membership test of
a billion items (that could be of arbitrary size). Moreover, the lookup is
very fast – it’s just 7 applications of the hash function. The constant lookup
cost is particularly attractive, as it doesn’t depend on the number of items
actually inserted, or on any particular pattern in the data (i.e. there are
no worst case scenarios with asymptotically higher cost).

On my machine, benchmarking with the Go implementation shown above I get ~30
nanoseconds per lookup. Mind you, this is the simplest Go implementation I
could think of – nothing here is optimized; I’m sure this can be improved at
least 2x by using a more speed-optimized hash implementation, for example.

Now imagine how long it would take to ascertain if data is present in a file
with 1 billion entries, even if the file contains proper indexing for fast
lookups. Just asking the OS to read the file’s first few KiBs to get at the
index would take orders of magnitude longer than 30 ns.

Recall that Bloom filters are best suited for cases “in which the great majority
of messages to be tested will not belong to the given set”. Moreover, even if
the data exists in the file, false positives only happen 1% of the time.
Therefore, the number of times we’ll have to go to the disk just to find the
data is not there is a very small fraction of total accesses.

Code

The full code for this post, with tests, is available
on GitHub.

Appendix: the Math behind Bloom filters

A reminder on notation:

• m: size (in bits) of the set
• n: how many keys were inserted into the filter
• k: number of hash functions used to insert/test each key

For a specific bit in the set, assuming our hash functions distribute
the keys randomly, the probability of it not being set by a specific
hash function is:

And the probability it’s not set by either of our k hash functions is:

The last formula is constructed to use an approximation of
for a large enough m (see the appendix in this post) to write:

After inserting n elements, the probability that it’s 0 is:

Meaning that the probability of it being 1 is:

Recap: this is the probability of any given bit being 1 after n bits
were inserted into a set of size m with k different hash functions.

Assuming independence between our hash functions (this is not super
rigorous, but a reasonable assumption in practice), let’s calculate the
false positive rate. Suppose we have a new key that’s not in the set,
and we’re trying to check its membership by hashing it with our k hash
functions. The false positive rate is the probability that all hashes
land on a bit that’s already set to 1:

This is also called the error rate of our filter, or
. To get an optimal (minimal) false positive rate,
let’s minimize . Since the logarithm function is
monotonically increasing, it will be more convenient to minimize
:

We’ll calculate the derivative w.r.t. k and set it to 0:

Substituting a variable and using some more
calculus and algebra, we can find that:

A numerical example: if we have a set with 1 million bits, and we expect
to insert about 100,000 elements, the optimal number of hash functions
is:

However, it’s more useful to aim for a certain error rate, and set the
filter parameters accordingly. Let’s assume we’ll be using this optimal
value of k. Substituting into the
equation for from above:

If we use the numerical example from before with ,
the error rate with an optimal k will be
.

What often happens is that we have an error rate in mind and we want to
calculate how many bits per element we want to dedicate in our set.
Let’s take the previous equation and try to isolate
from it using a logarithm:

Then:

Final numerical example: suppose we want an error (false positive) rate
of 1%. This means our set should have:

… bits per element. So if we expect about 100,000 elements, the bit
set used for our filter should have at least 958,000 bits. And, as
calculated earlier, we should be using hash functions to
achieve this optimal error rate.